http://www.maths.com/logarithms/index.php
This website is extremely useful. Please read and watch those videos. It's great for your revision and understanding. I hope you'll like it! enjoy~
Source: David, Cornelius. Math.com, 2010.
Wednesday, 9 November 2011
Logarithm and Physics?
Wow! You can call me a country bumpkin if you want so! This is the first time I know that Logarithm that i used to hate the most is so useful and it's actually relating to my beloved physic subject! Hahaha!
Logarithm is in everyday life. Basically this subtopic is just about applying logarithm into pH value, Decibel Scale and Ritcher Scale. It's important for us to memorize three important formulas in this subtopic.
1. pH = - log [ H+] , where H+ is the concentration of hydronium ions in moles/litre
Example: pH = - log (10-4) = - (-4) = +4
Therefor, the pH value for this solution is Acidic.
It's also important for you to know the pH scale! Don't mixed up with acidic and alkaline.

Refer to the diagram above if you are not so sure about pH scale.
For more information, please go to this website -----> Click me!!! :)
2. β 2 – β 1 = 10 log (I1 / I2) , where β 2 – β 1 is the difference in sound level, in decibels, and (I1 / I2) is the ratio of their sound intensities, where I is measured in watts per square metre (W/m2).
We need to be sure about the Decibel Scale too. Here i found you the scale of different sounds.

3. Ritcher Scale: M = log (I / I0), where M is the magnitude of earthquake, I is the intensity of earthquake and I0 is the intensity of standard earthquake.
A fun fact to share: In 1935 Charles Richter defined the magnitude of an earthquake to be ,
,
where I is the intensity of the earthquake (measured by the amplitude of a seismograph reading taken 100 km from the epicenter of the earthquake) and S is the intensity of a ''standard earthquake'' (whose amplitude is 1 micron =10-4 cm).
----------------------------------------------------------------------------------
When we are doing this subtopic, we used to see question comparing magnitude or dB and intensity of both Decibel Scale and Ritcher Scale. Please always remember that Comparing magnitude or dB and intensity are different! So, do not mixed up!
There are not much videos on the Internet. This is a video that i found it relevant to Logarithmic Scales in the Physical Sciences.
Source: AlRichards314, Youtube, 10 May 2009.
S.O.S. Math, "Application of Exponential and Logarithmic Function", 1999
Logarithm is in everyday life. Basically this subtopic is just about applying logarithm into pH value, Decibel Scale and Ritcher Scale. It's important for us to memorize three important formulas in this subtopic.
1. pH = - log [ H+] , where H+ is the concentration of hydronium ions in moles/litre
Example: pH = - log (10-4) = - (-4) = +4
Therefor, the pH value for this solution is Acidic.
It's also important for you to know the pH scale! Don't mixed up with acidic and alkaline.

Refer to the diagram above if you are not so sure about pH scale.
For more information, please go to this website -----> Click me!!! :)
2. β 2 – β 1 = 10 log (I1 / I2) , where β 2 – β 1 is the difference in sound level, in decibels, and (I1 / I2) is the ratio of their sound intensities, where I is measured in watts per square metre (W/m2).
We need to be sure about the Decibel Scale too. Here i found you the scale of different sounds.

3. Ritcher Scale: M = log (I / I0), where M is the magnitude of earthquake, I is the intensity of earthquake and I0 is the intensity of standard earthquake.
A fun fact to share: In 1935 Charles Richter defined the magnitude of an earthquake to be
 ,
,where I is the intensity of the earthquake (measured by the amplitude of a seismograph reading taken 100 km from the epicenter of the earthquake) and S is the intensity of a ''standard earthquake'' (whose amplitude is 1 micron =10-4 cm).
----------------------------------------------------------------------------------
When we are doing this subtopic, we used to see question comparing magnitude or dB and intensity of both Decibel Scale and Ritcher Scale. Please always remember that Comparing magnitude or dB and intensity are different! So, do not mixed up!
There are not much videos on the Internet. This is a video that i found it relevant to Logarithmic Scales in the Physical Sciences.
Source: AlRichards314, Youtube, 10 May 2009.
S.O.S. Math, "Application of Exponential and Logarithmic Function", 1999
Power Law of Logarithm
Morning people! Today, I'll be continue my advanced function blog with Power Law of Logarithm. Frankly, I think this is rather an easy logarithm law. I hope you guys will be having an easy time to understand, ingest and digest the knowledge I share today! :)
logbxn = nlogbx
for example: log(x-1) = -log(x)
log(x2) = 2log(x)
----------------------------------------------------------------------------------
Usually when we do logarithm exercises, we will encounter logarithmic equations or functions that have base other than 10. For instance, 2, 9, x, 0.5.... bla, bla, bla...
So, what we can do here is that to express the logarithmic function or equation using the change of base formula.
For example, logbm how are we going to evaluate it?
1. Make "log m" as the upper portion of a division.
2. Make "log b" as the lower portion of a division.
3. Combine both "log m" and "log b" into "log m / log b".
4. Now you can evaluate the answer using calculator or manually.
In conclusion, i scan the text book and I have the key concept of Power Law of Logarithm for you.
Source: PatrickJMT, Youtube 2011.
The Math Page "Topic in Precalculus"
logbxn = nlogbx
for example: log(x-1) = -log(x)
log(x2) = 2log(x)
----------------------------------------------------------------------------------
Usually when we do logarithm exercises, we will encounter logarithmic equations or functions that have base other than 10. For instance, 2, 9, x, 0.5.... bla, bla, bla...
So, what we can do here is that to express the logarithmic function or equation using the change of base formula.
For example, logbm how are we going to evaluate it?
1. Make "log m" as the upper portion of a division.
2. Make "log b" as the lower portion of a division.
3. Combine both "log m" and "log b" into "log m / log b".
4. Now you can evaluate the answer using calculator or manually.
In conclusion, i scan the text book and I have the key concept of Power Law of Logarithm for you.
For more exercises and information, please go to this link. Click me!!! :)
Watch this video!!! I love the way he explains how to change the base of logarithm! Clean and clear!
Source: PatrickJMT, Youtube 2011.
The Math Page "Topic in Precalculus"
Saturday, 5 November 2011
Transformation of Logarithmic Function.
Transformation of Logarithmic function is basically the same as transformation of polynomial function.
---------------------------------------------------------------------------------
I also found you a video about logarithmic transformation! This is a detailed video as he show us everything in step-by-step! Have great morning! XD
For more information, please visit this link -----> Click me!!! :)
The general form of form of logarithm is f(x) = a log [ k ( x - d ) ] + c
----------------------------------------------------------------------------------
When we do transformation we need to find an anchor point to be shown on the graph after we transformed the logarithmic function. I encourage you to find those easy points like (1, 0) or (10, 1). Move these original point in the equation y = log x after you add in other transformation.
---------------------------------------------------------------------------------
Steps to follow when we are doing transformation,
1. start from horizontal / vertical stretch / compression.
1. start from horizontal / vertical stretch / compression.
2. Then we continue with reflection (at either y-axis or x-axis).
3. Then, horizontal / vertical translation.
At last, it's important to add in the asymptote too! For logarithmic function, there is no horizontal asymptote as the range of logarithmic function is infinity. There is only vertical asymptote. State the point of the x-intercept and if there is y-intercept please state the point too.
----------------------------------------------------------------------------------
i took a photo of our text book. I hope it helps! :)
I also found you a video about logarithmic transformation! This is a detailed video as he show us everything in step-by-step! Have great morning! XD
For more information, please visit this link -----> Click me!!! :)
6.2 Lgarithm
Today, teacher taught us about the relationship between logarithm and exponential function. Before we start it is important that we refresh our mind with the Law of Logarithm.
-------------------------------------------------------------------------------------------------------------
When we chnaging the form of an exponential or logarithmic function, if you find hard to remember the changing process, why don't you try the "kick left, kick up" formula? It's just a formula to help you to remember how to change logarithmic function into exponential function and vice versa.
For example,
Rewrite the equation in logarithmic form:
4 = 22
First, kick the base 2 to the left hand side. Then, kick up the four to be the exponent. and you will have 24 = 2. Finally add in the "log" to the left hand side. The answer will be log2 4 = 2.
Example 2,
Rewrite the equation in exponential form.
2 = log416
Firs, kick the base 4 to the left and kick the 2 up. now yo will have 42 = log 16. take out the log, the answer will be 42 = 16.
----------------------------------------------------------------------------------
Another thing to remember is that
This will help you evaluating logarithmic function quickly without using calculator.
For example, log44 = 1.
---------------------------------------------------------------------------------
You might encounter another thing in logarithmic function is that you see log 50 or lg 50 without the base. Don't worry, just remember that common logarithms are logarithms with a base for common logarithms: log x means the same as log10x.
----------------------------------------------------------------------------------
Last but not least,
Rememeber that logarithm function is the inverse of exponential function and vice versa. Their graph are always in different direction where exponential graph is reflected at the y-axis to be the logarithmic graph and vice versa.
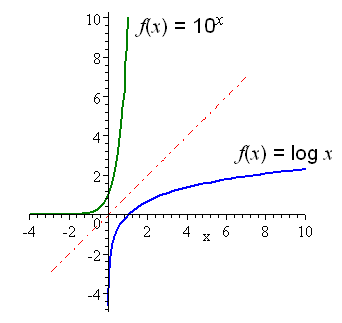
For more information, and some exercises I found you a website ----> Click me!!! :)
Enjoy~ out to pasar malam now! haha!
| bx by = bx+y | logb(xy) = logbx + logby |
| bx÷by = bx−y | logb(x/y) = logbx − logby |
| (bx)y = bxy | logb(xy) = y logbx |
-------------------------------------------------------------------------------------------------------------
When we chnaging the form of an exponential or logarithmic function, if you find hard to remember the changing process, why don't you try the "kick left, kick up" formula? It's just a formula to help you to remember how to change logarithmic function into exponential function and vice versa.
For example,
Rewrite the equation in logarithmic form:
4 = 22
First, kick the base 2 to the left hand side. Then, kick up the four to be the exponent. and you will have 24 = 2. Finally add in the "log" to the left hand side. The answer will be log2 4 = 2.
Example 2,
Rewrite the equation in exponential form.
2 = log416
Firs, kick the base 4 to the left and kick the 2 up. now yo will have 42 = log 16. take out the log, the answer will be 42 = 16.
----------------------------------------------------------------------------------
Another thing to remember is that
| b0 = 1 | logb1 = 0 |
| b1 = b | logbb = 1 |
This will help you evaluating logarithmic function quickly without using calculator.
For example, log44 = 1.
---------------------------------------------------------------------------------
You might encounter another thing in logarithmic function is that you see log 50 or lg 50 without the base. Don't worry, just remember that common logarithms are logarithms with a base for common logarithms: log x means the same as log10x.
----------------------------------------------------------------------------------
Last but not least,
Rememeber that logarithm function is the inverse of exponential function and vice versa. Their graph are always in different direction where exponential graph is reflected at the y-axis to be the logarithmic graph and vice versa.
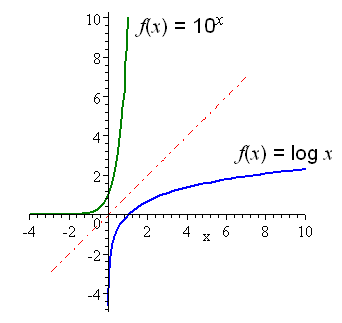
For more information, and some exercises I found you a website ----> Click me!!! :)
Enjoy~ out to pasar malam now! haha!
Friday, 4 November 2011
~Some thoughtful and inspirational Mathematical quotes~
I found a thoughtful quote from Facebook!!!! Make it your inspirational and motivational quote when you are CRACKING your head with your Advanced Functions' work and assignment!
"If people do not believe that mathematics is simple, it is only because they do not realize how complicated life is." ~John Louis von Neumann
This is truly indeed! If we are taking mathematics hard with a negative mind set, we will stuck in the sorrowful-mathematics-valley that you never able to climb up!
So, when you feel yourselves having a hard time dealing with maths work, here is another nice quote from my Advanced Functions lecturer,
"This is life!" ~ Ms. Joanne Ho
From my own interpretation, life is only beautiful if it is hard. Things won't be good, nice, awesome, worthy, meaning, successful if we never meet failure or obstacles in our life!
"If people do not believe that mathematics is simple, it is only because they do not realize how complicated life is." ~John Louis von Neumann
This is truly indeed! If we are taking mathematics hard with a negative mind set, we will stuck in the sorrowful-mathematics-valley that you never able to climb up!
So, when you feel yourselves having a hard time dealing with maths work, here is another nice quote from my Advanced Functions lecturer,
"This is life!" ~ Ms. Joanne Ho
From my own interpretation, life is only beautiful if it is hard. Things won't be good, nice, awesome, worthy, meaning, successful if we never meet failure or obstacles in our life!
Some useful videos about INVERSE-ing the Exponential Function!
This guy is showing both exponential functions y= bx and x = by that i mentioned is the 5.1 post. starting from 10th minute, he starts to teach the inverse of exponential function.
This young lady focuses on inverse of exponential function. She finishes teaching to transform exponential function into its inverse by 1:47 in the video and continues with inverse function which involve in Logarithm. Ig you find yourselves confused, just watch until 1:47 minute.
I hope these 2 videos help you from the exponential inverse MONSTER! haha! Good night! zzzz....
Source: AlRichards314 and Rip85hotmail, Youtube.
Thursday, 3 November 2011
6.1 The Exponential Function and Its Inverse
The general form of exponential function is y = bx
There are 2 forms if exponential function. First, y = bx where b>0, b≠1
For example, the graph below:
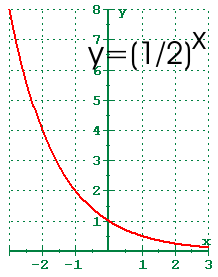
The second form of exponential function is y = bx where b>0
For example, the graph below:
&x=0003)
KEY FEATURES
Domain : {x ∈ R}
Range: {y = R, y>0}
y-intercept of 1
horizontal asymptote at y= 0
In conclusion, KEY FEATURES of exponential function are
- it has a repeating pattern of inite differences
- in the interval of b>1, the rate of change is increasing proportional to the function
- whereas, in the interval of 0<b<1, the rate of change is decreasing proportional to the function.
Now you know all the key features of exponential function. Here we move on to the inverse of exponential function!
The inverse function of y = bx x = by

There are 2 forms if exponential function. First, y = bx where b>0, b≠1
For example, the graph below:
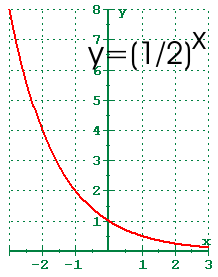
The second form of exponential function is y = bx where b>0
For example, the graph below:
KEY FEATURES
Domain : {x ∈ R}
Range: {y = R, y>0}
y-intercept of 1
horizontal asymptote at y= 0
In conclusion, KEY FEATURES of exponential function are
- it has a repeating pattern of inite differences
- in the interval of b>1, the rate of change is increasing proportional to the function
- whereas, in the interval of 0<b<1, the rate of change is decreasing proportional to the function.
Now you know all the key features of exponential function. Here we move on to the inverse of exponential function!
The inverse function of y = bx x = by

If you observe it, you actually can find that inverse exponential is reflected at the line y = x.
Please take notes that it's KEY FEATURES are different from exponential function.
Domain: { x ∈ R, x > 0 }
Range: {y ∈ R}
Please take notes that it's KEY FEATURES are different from exponential function.
Domain: { x ∈ R, x > 0 }
Range: {y ∈ R}
Vertical Asymptote at x = 0
For more information about logarithm and it's inverse, go to
this link, hope it helps!
For more information about logarithm and it's inverse, go to
this link, hope it helps!
Tuesday, 1 November 2011
It's back and for better!
Hey, hey, hey~ Yu Hang's back for Advanced Function's blog!
You know what, I don't really like Logarithm... I used to have fear with it. When i was form 4 and form 5 i had a great trauma with it. I used to have a mindset that it's real tough and i just don't happen to understand what LOGARITHM means to me.
Even when we started Chapter 6. I had a bit of nervous~ But, things don't really go too scary, creepy, haunting.... as i think! haha! I guess, my mind GREW! yeah!! maybe... Ms. Joanne's methodology works on me! anyway, I'm happy.
Logarithm? no wooooories~ come and fight! ACHA! HIYAK!

This is what I feel now. I failed quite some times last time when I was doing my Logarithm chapter in high school. But, now, I believed that I know it better!
Come on, let's go through the chapter 6 - Exponential and Logarithmic Function together! I hope I can give you some helpful information! Have a great day~
You know what, I don't really like Logarithm... I used to have fear with it. When i was form 4 and form 5 i had a great trauma with it. I used to have a mindset that it's real tough and i just don't happen to understand what LOGARITHM means to me.
Even when we started Chapter 6. I had a bit of nervous~ But, things don't really go too scary, creepy, haunting.... as i think! haha! I guess, my mind GREW! yeah!! maybe... Ms. Joanne's methodology works on me! anyway, I'm happy.
Logarithm? no wooooories~ come and fight! ACHA! HIYAK!

This is what I feel now. I failed quite some times last time when I was doing my Logarithm chapter in high school. But, now, I believed that I know it better!
Come on, let's go through the chapter 6 - Exponential and Logarithmic Function together! I hope I can give you some helpful information! Have a great day~
Friday, 2 September 2011
< > Inequalities ≤ ≥
This subtopic reminds me a lot of how my add math teacher, taught me doing the inequalities in the quadratic function. I used to forget and mix up with the sign changing of the inequality sign when negative turns positive and vice versa. Sometimes, I even felt Advanced Functions is a continuous of my secondary school add math class and it is also a subject that brings back a lot of beautiful memories of mine when I was in secondary school. But, one thing I prefer Advanced Functions is that it is way more interesting than add math. last time i used to do piles and piles of homework and practices. But, now things changed. We do mind maps and online activities. It's fun!!! That's why I'm doing my homework now... actually I should say blogging... hahaha!
OK! Enough for my the rubbish-like introduction take make a little sense but not too much sense... OMG... what I'm saying!
In this subtopic called "Solve Inequalities Using Technologies" I found out, we don't really use much technology like graphing calculator. But, we use different ways like number line method, graphing method and numeric method and 2 graph method.
First, the number line method.
For inequality sign "<" the arrow on the number line goes towards left as it is less than certain number.
For inequality sign ">" the arrow on the number line goes towards right as it is greater than certain number.
Watch this video about Graphing Inequalities on a Number Line.
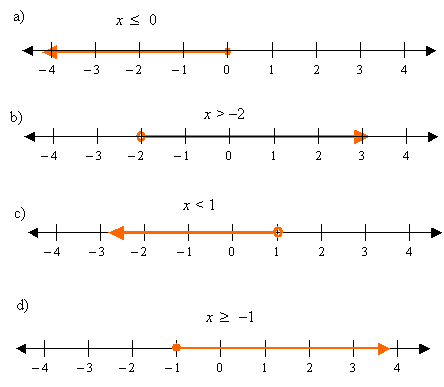
From the example above we noticed one thing. A fully colored dot and a hollow dot. What is the difference?
a fully colored dot on the number lines mean the sign "≤" or "≥" depending on the direction of the arrow. A hollow dot means the sign "<" and ">" depending on the direction of the arrow.
Second, the graphing method or the 2 graph method.
By looking at the graph we can know which part of the graph is above or below the x-axis. This method provides us an image of the range where the y-values are positive or negative and thus giving us the answer of the inequalities.
If we solve the inequalities using 2 graphs method, we need to make both side of the inequalities to be equal to y then plot 2 graphs. The x-value of the intersection point for both graphs will be the answer for the inequalities.
For a clearer understanding of graphing method, I suggest you to go to this link. http://www.sosmath.com/algebra/inequalities/ineq04/ineq04.html. I think it is pretty informative and clear.
For the last method, Numerical method, I found it the best method. I do not know why, i just like it the most. That's why people says "love is blind"... haha!
First we transform the inequalities into an equation that is equal to 0. Then, we look for its x-intercept. Then we test each interval of the x-intercept.
Let's say for example the x-intercept are -6 and 2, we can try out when x<-6, the function is either positive or negative. Then the interval between -6<x<2 and x>2.
Then we look for the interval that is positive or negative, according to the sign of the inequalities in the question, and that interval will be our answer. For example, for question "solve x³+2x-1>0" we will look for the positive part of the function as the sign is greater than and vice versa for question with a less than sign.
Web resources:
Youtube, Graphing Inequalities on a Number Line, <http://www.youtube.com/watch?v=AjZzACaeIco&feature=player_embedded>
S.O.S Math, Solving Polynomial Inequalities by Graphing, <http://www.sosmath.com/algebra/inequalities/ineq04/ineq04.html>
OK! Enough for my the rubbish-like introduction take make a little sense but not too much sense... OMG... what I'm saying!
In this subtopic called "Solve Inequalities Using Technologies" I found out, we don't really use much technology like graphing calculator. But, we use different ways like number line method, graphing method and numeric method and 2 graph method.
First, the number line method.
For inequality sign "<" the arrow on the number line goes towards left as it is less than certain number.
For inequality sign ">" the arrow on the number line goes towards right as it is greater than certain number.
Watch this video about Graphing Inequalities on a Number Line.

From the example above we noticed one thing. A fully colored dot and a hollow dot. What is the difference?
a fully colored dot on the number lines mean the sign "≤" or "≥" depending on the direction of the arrow. A hollow dot means the sign "<" and ">" depending on the direction of the arrow.
Second, the graphing method or the 2 graph method.
By looking at the graph we can know which part of the graph is above or below the x-axis. This method provides us an image of the range where the y-values are positive or negative and thus giving us the answer of the inequalities.
If we solve the inequalities using 2 graphs method, we need to make both side of the inequalities to be equal to y then plot 2 graphs. The x-value of the intersection point for both graphs will be the answer for the inequalities.
For a clearer understanding of graphing method, I suggest you to go to this link. http://www.sosmath.com/algebra/inequalities/ineq04/ineq04.html. I think it is pretty informative and clear.
For the last method, Numerical method, I found it the best method. I do not know why, i just like it the most. That's why people says "love is blind"... haha!
First we transform the inequalities into an equation that is equal to 0. Then, we look for its x-intercept. Then we test each interval of the x-intercept.
Let's say for example the x-intercept are -6 and 2, we can try out when x<-6, the function is either positive or negative. Then the interval between -6<x<2 and x>2.
Then we look for the interval that is positive or negative, according to the sign of the inequalities in the question, and that interval will be our answer. For example, for question "solve x³+2x-1>0" we will look for the positive part of the function as the sign is greater than and vice versa for question with a less than sign.
Web resources:
Youtube, Graphing Inequalities on a Number Line, <http://www.youtube.com/watch?v=AjZzACaeIco&feature=player_embedded>
S.O.S Math, Solving Polynomial Inequalities by Graphing, <http://www.sosmath.com/algebra/inequalities/ineq04/ineq04.html>
What?! Polynomial Functions has its Family?
In a family, we have some similarities with our parents and siblings and other relatives. It can be the physical appearance or the characteristic. Same goes to the Polynomial equation of a family! I know, you might think what I am talking about absolute ridiculous rubbish. Hahaha~ chill~
First of all, let me explain what is the families of polynomial functions. A polynomial function that belongs to a family have the same characteristic. Polynomial function of the same family have the same x-intercept, roots, and zeros.
Example:
f(x)=(x+1) (x-1) (x+3) and
f(x)=2(x+1) (x-1) (x+3)
belong to the same family because they have the same x-intercepts, roots and zeros.
Example 2:
Three polynomial equations above are of the same family because they have the same x-intercept of 2 and 5.
To determine the equation of the particular member of the family, the only thing that we require is any one point on the graph. We can substitute the x value or y-value into the function and find out the variable that differs the shape of the graph.
In general, polynomial functions of the same family can be represented in the form,
y = k( x - a₁ ) ( x - a₂ )...( x - an ), where k ∈ R, k ≠ 0.
Birds of a feather flock together.
Polynomial equation of a family, share the same x-intercept together.
See? I told you polynomial functions have their own family. Haha! Enjoy~
Web resource:The Family of Quadratic Functions <http://www.glencoe.com/sec/math/algebra/algebra1/algebra1_08/other_calculator_keystrokes/472_Alg1_9-1B_873823_CFX.pdf>
First of all, let me explain what is the families of polynomial functions. A polynomial function that belongs to a family have the same characteristic. Polynomial function of the same family have the same x-intercept, roots, and zeros.
Example:
f(x)=(x+1) (x-1) (x+3) and
f(x)=2(x+1) (x-1) (x+3)
belong to the same family because they have the same x-intercepts, roots and zeros.
Example 2:
Three polynomial equations above are of the same family because they have the same x-intercept of 2 and 5.
To determine the equation of the particular member of the family, the only thing that we require is any one point on the graph. We can substitute the x value or y-value into the function and find out the variable that differs the shape of the graph.
In general, polynomial functions of the same family can be represented in the form,
y = k( x - a₁ ) ( x - a₂ )...( x - an ), where k ∈ R, k ≠ 0.
Birds of a feather flock together.
Polynomial equation of a family, share the same x-intercept together.
See? I told you polynomial functions have their own family. Haha! Enjoy~
Web resource:The Family of Quadratic Functions <http://www.glencoe.com/sec/math/algebra/algebra1/algebra1_08/other_calculator_keystrokes/472_Alg1_9-1B_873823_CFX.pdf>
Zer0, Roots and x-intercept. What's Their Relationship???
After I learned the Chapter 2.3, the question of "what's the difference and relationship between zero, root, and x-intercept?" pop in my mind. Why do they have different names yet they are almost the same????? Weird right? :P
Then. I found out they are actually interrelated and they are same in terms of its value.
Let's say for example the graph below.

The x-intercept on the graph is the zero of the graph and the polynomial equation; the zero of the graph is the factor of the polynomial equation; the x-intercept and zero are the roots of the polynomial equation. Thus, the zero, roots and x-intercepts are -1 and 5 (as from the graph above).
BUT, this is only for those polynomial equation that is factorable. For those polynomial equation that are not factorable, we can find out their zero or roots or x-intercept (if they have roots), we need to use the quadratic formula

or by using our graphing calculator.
Therefore, as a conclusion:
The Math Page, "The Roots, or Zeros, of a Polynomial" <http://www.themathpage.com/aprecalc/roots-zeros-polynomial.htm>
Then. I found out they are actually interrelated and they are same in terms of its value.
Let's say for example the graph below.

The x-intercept on the graph is the zero of the graph and the polynomial equation; the zero of the graph is the factor of the polynomial equation; the x-intercept and zero are the roots of the polynomial equation. Thus, the zero, roots and x-intercepts are -1 and 5 (as from the graph above).
BUT, this is only for those polynomial equation that is factorable. For those polynomial equation that are not factorable, we can find out their zero or roots or x-intercept (if they have roots), we need to use the quadratic formula

or by using our graphing calculator.
Therefore, as a conclusion:
- the real roots of a polynomial equation P(x)=0 is similar to the x-intercept of the graph P(x) and vice versa.
- A factorable polynomial equation's roots are equal to its zero and thus solving the factor of it.
- BUT, when we come to polynomial equation that is not factorable, we need to solve it using technology or by using graphing method.
Web resources: Wikipedia, "Zero of a Function" <http://en.wikipedia.org/wiki/Zero_of_a_function>
The Math Page, "The Roots, or Zeros, of a Polynomial" <http://www.themathpage.com/aprecalc/roots-zeros-polynomial.htm>
The Factor Theorem
When I learn about Factor Theorem, I found four things that I think are the essence of the theorem.
Web resources: Youtube, "The Factor Theorem, ExamSolution", <http://www.youtube.com/watch?v=6G3iAgpK4kA&feature=player_embedded>
Purplemath, "The Factor Theorem", <http://www.purplemath.com/modules/factrthm.htm>
First, the factor theorem itself. A brief and quick summary for it:
Fourth, the grouping factorization method. I found this method is quite convenient but it is different from what we (Malaysia national education system's students) learn in form 4 and 5. Don't freak out, you will find it easy after you read the following.
Grouping factorization method can be applied when pairs of term of polynomial can be grouped to factor out a common factor so that the resulting binomial factors are the same.
Example:
f(x)= x³ + 2x² - 9x -18. <~ group out the binomial factors
= x² (x + 2) - 9 (x + 2) <~ group the remaining numbers
= (x + 2) ( x² - 9 ) <~ factorize the factor that has power that is great than 1
= (x + 2) (x + 3) (x - 3 ) <~ DONE ^^
x-b is a factor of a polynomial P(x) if and only if P(b)=0.
Similarly, ax-b is a factor of P(x) if and only if P(b/a)=0.
Note: the acronym I learnt in the class is "iff" short form of if and only if. So don't be shock if you see your Advanced Function teacher write iff! Definitely not spelling error. =D
Example:
x-1 is the factor of P(x)= x³ + 4x² + x - 6 because P(1) = 0
x+1 is not the factor of P(x)= x³ + 4x² + x - 6 because P(-1) = 0
Second, the integral zero theorem. A brief explanation of this theorem:
If x-b is a factor of a polynomial function P(x) with leading coefficient 1 and remaining coefficient that are integers, then b is a factor of the constant term of P(x).
Thus, as a summary of this theorem, the word zero means the value of b when polynomial function P(x)=0.
Example:
P(x)= x³ + 2x² - 5x - 6
According to the Integral Zero Theorem, the possible factors of the constant term of P(x) MIGHT BE the possible factor in the form of x-b of P(x).
So, the zeroes of the constant term are: ±1, ±2, ±3 and ±6. After that, substitute all those zeroes into P(x). In this case, the zeroes that make P(x)=0 are -3, -1 and 2. Thus, the factors are x+3, x+1, and x-2.
Third, the Rational Zero Theorem. A brief explanation on it:
P(x) is a polynomial function with all integers coefficient and a leading coefficient that is greater than 1 or not an integer, x=b/ is the zero of P(x) where a and b are integers. Then,
- b is the factor of the constant term,
- a is the factor of the leading coefficient,
- ax-b is the factor of P(x).
Example:
The polynomial function of P(x)= 3x³ + 2x² - 7x + 2 needs Rational Zero Theorem to solve it.
The factors of the leading coefficient are ±1 and ±3. The factors of the constant term are ±1 and ±2. Thus, the possible combination of zeroes that can make P(b/a) are ±1/1, ±1/2, ±3/1 and ±3/2. In this case, the zeroes that make P(b/a)=0 are 1, -2 and 1/3. Thus, the factors of P(x) are x-1, x+2 and 3x-1.
Fourth, the grouping factorization method. I found this method is quite convenient but it is different from what we (Malaysia national education system's students) learn in form 4 and 5. Don't freak out, you will find it easy after you read the following.
Grouping factorization method can be applied when pairs of term of polynomial can be grouped to factor out a common factor so that the resulting binomial factors are the same.
Example:
f(x)= x³ + 2x² - 9x -18. <~ group out the binomial factors
= x² (x + 2) - 9 (x + 2) <~ group the remaining numbers
= (x + 2) ( x² - 9 ) <~ factorize the factor that has power that is great than 1
= (x + 2) (x + 3) (x - 3 ) <~ DONE ^^
That's it for the Factor Theorem. If you worry I make you blur (definitely I hope I'm not!!!), just youtube-ing the video below. I found it very useful. Thanks for reading and "digesting" what I posted!
Web resources: Youtube, "The Factor Theorem, ExamSolution", <http://www.youtube.com/watch?v=6G3iAgpK4kA&feature=player_embedded>
Purplemath, "The Factor Theorem", <http://www.purplemath.com/modules/factrthm.htm>
A cute little song to relax~
Hello people, I found a cute little song. I like the last line that says, "Yes try as you may,you just can't get away FROM MATHEMATICS." Personally, I am the type of person who can't get away of maths if I could not get it solved! Is it quite sad to hear. But, no pain, no gain. The more I suffer as a result I can't get it away, the more the satisfaction I got from it once I get it solved! I think all maths freak are the same! gimme 5! piakkkk! XD
Web resource: Youtube, "Math song", <http://www.youtube.com/watch?v=ZPMRA4yFeeM>
The Remainder Theorem
REMAINDER THEOREM is a way for us to solve polynomial equations in order to get us the remainder or to check its factor.
Example,
P(x) = 2x³ - 2x² - 3x + 3
This function can be either solved by using long division with factor of x - b where b is a real number or solve by using Remainder Theorem by substituting the value of b into P(x) where x = b from the factor of x - b into P(x). For example, when x - 2 is the factor of P(x), then x = 2. Then, substituting x = 2 into P(x).
P(x) = 2x³ - 2x² - 3x + 3
P(2) = 2(2)³ - 2(2)² - 3(2) + 3
P(2) = -1
Thus, the remainder is -1.
Thus, the Remainder Theorem:
when a polynomial function of P(x) is divided by x-b, the remainder is P(b). where b is an integers.
iExmaple 2:
P(x) = 2x³ - 2x² - 3x + 3, divisor, 2x-3
When the divisor has a leading coefficient that is not 1, then we assume the leading coefficient as "a" and the constant as "b". Thus, x=b/a.
P(x) = 2x³ - 2x² - 3x + 3
P(3/2) = 2(3/2)³ - 2(3/2)² - 3(3/2) + 3
P(3/2) = Remainder
Thus, the Remainder Theorem:
when a polynomial function of P(x) is divided by ax-b, the remainder is P(b/a). where b and a are integers.
There are two things that we need to remember. To write the result we got after doing long division or solving using remainder theorem, there are 2 ways. It can be either in quotient form or statement form (can used to check the division)
Let Q(x) be the quotient,
R be the remainder;
P(x) be the polynomial function;
x-b be the divisor
quotient form : P(x) = Q(x) + R
x-b x-b
statement : P(x)= [Q(x)] [(x-b)] + R
If we wanna explain the remainder geometrically, the quotient is actually the slope of secant between point (b, P(b)) and (x, P(x))
to get a better concept of Remainder Theorem, I found you all a video.
This is an easy theory, so, just make use of it well. enjoy~ Thanks for reading!
Web resources: Youtube, "The Remainder Theorem, Exmaple 2", <http://www.youtube.com/watch?v=q57NU29KNGw>
Purplemath, "The Remainder Theorem", <http://www.purplemath.com/modules/remaindr.htm>
Example,
P(x) = 2x³ - 2x² - 3x + 3
This function can be either solved by using long division with factor of x - b where b is a real number or solve by using Remainder Theorem by substituting the value of b into P(x) where x = b from the factor of x - b into P(x). For example, when x - 2 is the factor of P(x), then x = 2. Then, substituting x = 2 into P(x).
P(x) = 2x³ - 2x² - 3x + 3
P(2) = 2(2)³ - 2(2)² - 3(2) + 3
P(2) = -1
Thus, the remainder is -1.
Thus, the Remainder Theorem:
when a polynomial function of P(x) is divided by x-b, the remainder is P(b). where b is an integers.
iExmaple 2:
P(x) = 2x³ - 2x² - 3x + 3, divisor, 2x-3
When the divisor has a leading coefficient that is not 1, then we assume the leading coefficient as "a" and the constant as "b". Thus, x=b/a.
P(x) = 2x³ - 2x² - 3x + 3
P(3/2) = 2(3/2)³ - 2(3/2)² - 3(3/2) + 3
P(3/2) = Remainder
Thus, the Remainder Theorem:
when a polynomial function of P(x) is divided by ax-b, the remainder is P(b/a). where b and a are integers.
There are two things that we need to remember. To write the result we got after doing long division or solving using remainder theorem, there are 2 ways. It can be either in quotient form or statement form (can used to check the division)
Let Q(x) be the quotient,
R be the remainder;
P(x) be the polynomial function;
x-b be the divisor
quotient form : P(x) = Q(x) + R
x-b x-b
statement : P(x)= [Q(x)] [(x-b)] + R
If we wanna explain the remainder geometrically, the quotient is actually the slope of secant between point (b, P(b)) and (x, P(x))
to get a better concept of Remainder Theorem, I found you all a video.
This is an easy theory, so, just make use of it well. enjoy~ Thanks for reading!
Web resources: Youtube, "The Remainder Theorem, Exmaple 2", <http://www.youtube.com/watch?v=q57NU29KNGw>
Purplemath, "The Remainder Theorem", <http://www.purplemath.com/modules/remaindr.htm>
Before we start...
The first day we started Chapter 2, we learned about long division which Ms. Joanne (our Advanced Functions teacher) call it "Long way". This "long way" makes everyone in my class burst of laughing because we have a friend in the class called, Long Wei! It's the same pronunciation. Sorry Long Wei, no offense~

This might look childish and you take it very easy as you learn it since you were in primary school. But, never underestimate it. It is so important throughout this chapter. Haha!
A brief description:
68 is the dividend;
2 is the divisor;
34 is the quotient;
and 8 is the remainder.
When you are doing long division, you must be very careful. A small careless mistake might get you a wrong answer. So, we must times the divisor and quotient meticulously, and minus the answer carefully.
For more information, go to this link, http://en.wikipedia.org/wiki/Long_division. I hope it helps you!
Web resources: Wikipedia, "Long Division", <http://en.wikipedia.org/wiki/Long_division>
Purplemath, "Polynomial Long Division", <http://www.purplemath.com/modules/polydiv2.htm>
Back to the topic, long division is the prerequisite skill for us to learn remainder theorem and factor theorem. We will need it very much in solving polynomial equation in this chapter.

This might look childish and you take it very easy as you learn it since you were in primary school. But, never underestimate it. It is so important throughout this chapter. Haha!
A brief description:
68 is the dividend;
2 is the divisor;
34 is the quotient;
and 8 is the remainder.
When you are doing long division, you must be very careful. A small careless mistake might get you a wrong answer. So, we must times the divisor and quotient meticulously, and minus the answer carefully.
For more information, go to this link, http://en.wikipedia.org/wiki/Long_division. I hope it helps you!
Web resources: Wikipedia, "Long Division", <http://en.wikipedia.org/wiki/Long_division>
Purplemath, "Polynomial Long Division", <http://www.purplemath.com/modules/polydiv2.htm>
~The Grand Opening~
Hi, everyone! This is my first ever blog and i give it to my CPU's Advanced Function. I hope I do it well. XD Basically, this is a blog for everyone to discuss about advanced functions. In this blog, I'll emphasize on the Unit 2 of the Advanced Function from what I learned from Ms. Joanne, my dear teacher. I do not want the blog to be too dull and academic-like. Instead, I hope it is a great place for everyone to come and comment and get some handy tips or information about Advanced Function.
Advanced Function isn't something dry and boring and scary and just numberS! So, enjoy! HANG ON! IT'S ADVANCED FUNCTION lah~ ^^
Advanced Function isn't something dry and boring and scary and just numberS! So, enjoy! HANG ON! IT'S ADVANCED FUNCTION lah~ ^^
Subscribe to:
Comments (Atom)



