6.1 The Exponential Function and Its Inverse

The general form of exponential function is y = b^x

There are 2 forms if exponential function. First, y = b^x where b>0, b≠1


For example, the graph below:

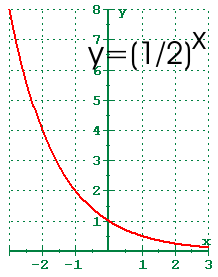
The second form of exponential function is y = b^x where b>0


For example, the graph below:
 

KEY FEATURES

Domain : {x ∈ R}


Range: {y = R, y>0}

y-intercept of 1

horizontal asymptote at y= 0


In conclusion, KEY FEATURES of exponential function are




 - it has a repeating pattern of inite differences
 - in the interval of b>1, the rate of change is increasing proportional to the function
 - whereas, in the interval of 0<b<1, the rate of change is decreasing proportional to the function. 

Now you know all the key features of exponential function. Here we move on to the inverse of exponential function!
The inverse function of y = b^x  x = b^y

If you observe it, you actually can find that inverse exponential is reflected at the line y = x.

Please take notes that it's KEY FEATURES are different from exponential function.

Domain: { x ∈ R, x > 0 }

Range: {y ∈ R}

Vertical Asymptote at x = 0

For more information about logarithm and it's inverse, go to

this link, hope it helps! 

Click me! :)