6.2 Lgarithm

Today, teacher taught us about the relationship between logarithm and exponential function. Before we start it is important that we refresh our mind with the Law of Logarithm. 

bx by = bx+y	logb(xy) = logbx + logby
bx÷by = bx−y	logb(x/y) = logbx − logby
(bx)y = bxy	logb(xy) = y logbx

-------------------------------------------------------------------------------------------------------------


When we chnaging the form of an exponential or logarithmic function, if you find hard to remember the changing process, why don't you try the "kick left, kick up" formula? It's just a formula to help you to remember how to change logarithmic function into exponential function and vice versa.


For example,
Rewrite the equation in logarithmic form:
4 = 2²



 First, kick the base 2 to the left hand side. Then, kick up the four to be the exponent. and you will have 2⁴ = 2. Finally add in the "log" to the left hand side. The answer will be log₂ 4 = 2. 

Example 2, 
Rewrite the equation in exponential form.
2 = log₄16

Firs, kick the base 4 to the left and kick the 2 up. now yo will have 4² = log 16. take out the log, the answer will be 4² = 16.





----------------------------------------------------------------------------------


Another thing to remember is that

b0 = 1	logb1 = 0
b1 = b	logbb = 1

This will help you evaluating logarithmic function quickly without using calculator.

For example, log₄4 = 1.
 ---------------------------------------------------------------------------------

You might encounter another thing in logarithmic function is that you see log 50 or lg 50 without the base. Don't worry, just remember that common logarithms are logarithms with a base for common logarithms: log x means the same as log₁₀x.


----------------------------------------------------------------------------------


Last but not least,

Rememeber that logarithm function is the inverse of exponential function and vice versa. Their graph are always in different direction where exponential graph is reflected at the y-axis to be the logarithmic graph and vice versa.


  


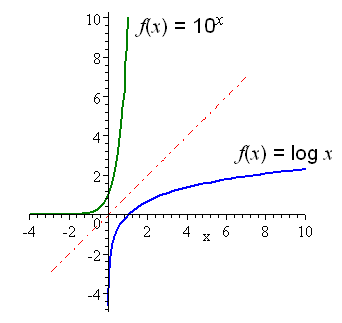
For more information, and some exercises I found you a website ----> Click me!!! :)


Enjoy~ out to pasar malam now! haha!