http://www.maths.com/logarithms/index.php
This website is extremely useful. Please read and watch those videos. It's great for your revision and understanding. I hope you'll like it! enjoy~
Source: David, Cornelius. Math.com, 2010.
Wednesday, 9 November 2011
Logarithm and Physics?
Wow! You can call me a country bumpkin if you want so! This is the first time I know that Logarithm that i used to hate the most is so useful and it's actually relating to my beloved physic subject! Hahaha!
Logarithm is in everyday life. Basically this subtopic is just about applying logarithm into pH value, Decibel Scale and Ritcher Scale. It's important for us to memorize three important formulas in this subtopic.
1. pH = - log [ H+] , where H+ is the concentration of hydronium ions in moles/litre
Example: pH = - log (10-4) = - (-4) = +4
Therefor, the pH value for this solution is Acidic.
It's also important for you to know the pH scale! Don't mixed up with acidic and alkaline.

Refer to the diagram above if you are not so sure about pH scale.
For more information, please go to this website -----> Click me!!! :)
2. β 2 – β 1 = 10 log (I1 / I2) , where β 2 – β 1 is the difference in sound level, in decibels, and (I1 / I2) is the ratio of their sound intensities, where I is measured in watts per square metre (W/m2).
We need to be sure about the Decibel Scale too. Here i found you the scale of different sounds.

3. Ritcher Scale: M = log (I / I0), where M is the magnitude of earthquake, I is the intensity of earthquake and I0 is the intensity of standard earthquake.
A fun fact to share: In 1935 Charles Richter defined the magnitude of an earthquake to be ,
,
where I is the intensity of the earthquake (measured by the amplitude of a seismograph reading taken 100 km from the epicenter of the earthquake) and S is the intensity of a ''standard earthquake'' (whose amplitude is 1 micron =10-4 cm).
----------------------------------------------------------------------------------
When we are doing this subtopic, we used to see question comparing magnitude or dB and intensity of both Decibel Scale and Ritcher Scale. Please always remember that Comparing magnitude or dB and intensity are different! So, do not mixed up!
There are not much videos on the Internet. This is a video that i found it relevant to Logarithmic Scales in the Physical Sciences.
Source: AlRichards314, Youtube, 10 May 2009.
S.O.S. Math, "Application of Exponential and Logarithmic Function", 1999
Logarithm is in everyday life. Basically this subtopic is just about applying logarithm into pH value, Decibel Scale and Ritcher Scale. It's important for us to memorize three important formulas in this subtopic.
1. pH = - log [ H+] , where H+ is the concentration of hydronium ions in moles/litre
Example: pH = - log (10-4) = - (-4) = +4
Therefor, the pH value for this solution is Acidic.
It's also important for you to know the pH scale! Don't mixed up with acidic and alkaline.

Refer to the diagram above if you are not so sure about pH scale.
For more information, please go to this website -----> Click me!!! :)
2. β 2 – β 1 = 10 log (I1 / I2) , where β 2 – β 1 is the difference in sound level, in decibels, and (I1 / I2) is the ratio of their sound intensities, where I is measured in watts per square metre (W/m2).
We need to be sure about the Decibel Scale too. Here i found you the scale of different sounds.

3. Ritcher Scale: M = log (I / I0), where M is the magnitude of earthquake, I is the intensity of earthquake and I0 is the intensity of standard earthquake.
A fun fact to share: In 1935 Charles Richter defined the magnitude of an earthquake to be
 ,
,where I is the intensity of the earthquake (measured by the amplitude of a seismograph reading taken 100 km from the epicenter of the earthquake) and S is the intensity of a ''standard earthquake'' (whose amplitude is 1 micron =10-4 cm).
----------------------------------------------------------------------------------
When we are doing this subtopic, we used to see question comparing magnitude or dB and intensity of both Decibel Scale and Ritcher Scale. Please always remember that Comparing magnitude or dB and intensity are different! So, do not mixed up!
There are not much videos on the Internet. This is a video that i found it relevant to Logarithmic Scales in the Physical Sciences.
Source: AlRichards314, Youtube, 10 May 2009.
S.O.S. Math, "Application of Exponential and Logarithmic Function", 1999
Power Law of Logarithm
Morning people! Today, I'll be continue my advanced function blog with Power Law of Logarithm. Frankly, I think this is rather an easy logarithm law. I hope you guys will be having an easy time to understand, ingest and digest the knowledge I share today! :)
logbxn = nlogbx
for example: log(x-1) = -log(x)
log(x2) = 2log(x)
----------------------------------------------------------------------------------
Usually when we do logarithm exercises, we will encounter logarithmic equations or functions that have base other than 10. For instance, 2, 9, x, 0.5.... bla, bla, bla...
So, what we can do here is that to express the logarithmic function or equation using the change of base formula.
For example, logbm how are we going to evaluate it?
1. Make "log m" as the upper portion of a division.
2. Make "log b" as the lower portion of a division.
3. Combine both "log m" and "log b" into "log m / log b".
4. Now you can evaluate the answer using calculator or manually.
In conclusion, i scan the text book and I have the key concept of Power Law of Logarithm for you.
Source: PatrickJMT, Youtube 2011.
The Math Page "Topic in Precalculus"
logbxn = nlogbx
for example: log(x-1) = -log(x)
log(x2) = 2log(x)
----------------------------------------------------------------------------------
Usually when we do logarithm exercises, we will encounter logarithmic equations or functions that have base other than 10. For instance, 2, 9, x, 0.5.... bla, bla, bla...
So, what we can do here is that to express the logarithmic function or equation using the change of base formula.
For example, logbm how are we going to evaluate it?
1. Make "log m" as the upper portion of a division.
2. Make "log b" as the lower portion of a division.
3. Combine both "log m" and "log b" into "log m / log b".
4. Now you can evaluate the answer using calculator or manually.
In conclusion, i scan the text book and I have the key concept of Power Law of Logarithm for you.
For more exercises and information, please go to this link. Click me!!! :)
Watch this video!!! I love the way he explains how to change the base of logarithm! Clean and clear!
Source: PatrickJMT, Youtube 2011.
The Math Page "Topic in Precalculus"
Saturday, 5 November 2011
Transformation of Logarithmic Function.
Transformation of Logarithmic function is basically the same as transformation of polynomial function.
---------------------------------------------------------------------------------
I also found you a video about logarithmic transformation! This is a detailed video as he show us everything in step-by-step! Have great morning! XD
For more information, please visit this link -----> Click me!!! :)
The general form of form of logarithm is f(x) = a log [ k ( x - d ) ] + c
----------------------------------------------------------------------------------
When we do transformation we need to find an anchor point to be shown on the graph after we transformed the logarithmic function. I encourage you to find those easy points like (1, 0) or (10, 1). Move these original point in the equation y = log x after you add in other transformation.
---------------------------------------------------------------------------------
Steps to follow when we are doing transformation,
1. start from horizontal / vertical stretch / compression.
1. start from horizontal / vertical stretch / compression.
2. Then we continue with reflection (at either y-axis or x-axis).
3. Then, horizontal / vertical translation.
At last, it's important to add in the asymptote too! For logarithmic function, there is no horizontal asymptote as the range of logarithmic function is infinity. There is only vertical asymptote. State the point of the x-intercept and if there is y-intercept please state the point too.
----------------------------------------------------------------------------------
i took a photo of our text book. I hope it helps! :)
I also found you a video about logarithmic transformation! This is a detailed video as he show us everything in step-by-step! Have great morning! XD
For more information, please visit this link -----> Click me!!! :)
6.2 Lgarithm
Today, teacher taught us about the relationship between logarithm and exponential function. Before we start it is important that we refresh our mind with the Law of Logarithm.
-------------------------------------------------------------------------------------------------------------
When we chnaging the form of an exponential or logarithmic function, if you find hard to remember the changing process, why don't you try the "kick left, kick up" formula? It's just a formula to help you to remember how to change logarithmic function into exponential function and vice versa.
For example,
Rewrite the equation in logarithmic form:
4 = 22
First, kick the base 2 to the left hand side. Then, kick up the four to be the exponent. and you will have 24 = 2. Finally add in the "log" to the left hand side. The answer will be log2 4 = 2.
Example 2,
Rewrite the equation in exponential form.
2 = log416
Firs, kick the base 4 to the left and kick the 2 up. now yo will have 42 = log 16. take out the log, the answer will be 42 = 16.
----------------------------------------------------------------------------------
Another thing to remember is that
This will help you evaluating logarithmic function quickly without using calculator.
For example, log44 = 1.
---------------------------------------------------------------------------------
You might encounter another thing in logarithmic function is that you see log 50 or lg 50 without the base. Don't worry, just remember that common logarithms are logarithms with a base for common logarithms: log x means the same as log10x.
----------------------------------------------------------------------------------
Last but not least,
Rememeber that logarithm function is the inverse of exponential function and vice versa. Their graph are always in different direction where exponential graph is reflected at the y-axis to be the logarithmic graph and vice versa.
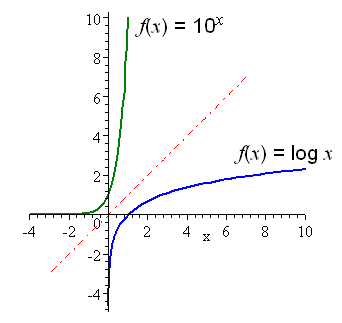
For more information, and some exercises I found you a website ----> Click me!!! :)
Enjoy~ out to pasar malam now! haha!
| bx by = bx+y | logb(xy) = logbx + logby |
| bx÷by = bx−y | logb(x/y) = logbx − logby |
| (bx)y = bxy | logb(xy) = y logbx |
-------------------------------------------------------------------------------------------------------------
When we chnaging the form of an exponential or logarithmic function, if you find hard to remember the changing process, why don't you try the "kick left, kick up" formula? It's just a formula to help you to remember how to change logarithmic function into exponential function and vice versa.
For example,
Rewrite the equation in logarithmic form:
4 = 22
First, kick the base 2 to the left hand side. Then, kick up the four to be the exponent. and you will have 24 = 2. Finally add in the "log" to the left hand side. The answer will be log2 4 = 2.
Example 2,
Rewrite the equation in exponential form.
2 = log416
Firs, kick the base 4 to the left and kick the 2 up. now yo will have 42 = log 16. take out the log, the answer will be 42 = 16.
----------------------------------------------------------------------------------
Another thing to remember is that
| b0 = 1 | logb1 = 0 |
| b1 = b | logbb = 1 |
This will help you evaluating logarithmic function quickly without using calculator.
For example, log44 = 1.
---------------------------------------------------------------------------------
You might encounter another thing in logarithmic function is that you see log 50 or lg 50 without the base. Don't worry, just remember that common logarithms are logarithms with a base for common logarithms: log x means the same as log10x.
----------------------------------------------------------------------------------
Last but not least,
Rememeber that logarithm function is the inverse of exponential function and vice versa. Their graph are always in different direction where exponential graph is reflected at the y-axis to be the logarithmic graph and vice versa.
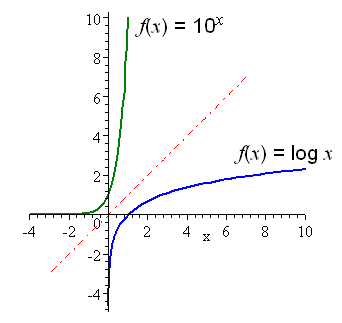
For more information, and some exercises I found you a website ----> Click me!!! :)
Enjoy~ out to pasar malam now! haha!
Friday, 4 November 2011
~Some thoughtful and inspirational Mathematical quotes~
I found a thoughtful quote from Facebook!!!! Make it your inspirational and motivational quote when you are CRACKING your head with your Advanced Functions' work and assignment!
"If people do not believe that mathematics is simple, it is only because they do not realize how complicated life is." ~John Louis von Neumann
This is truly indeed! If we are taking mathematics hard with a negative mind set, we will stuck in the sorrowful-mathematics-valley that you never able to climb up!
So, when you feel yourselves having a hard time dealing with maths work, here is another nice quote from my Advanced Functions lecturer,
"This is life!" ~ Ms. Joanne Ho
From my own interpretation, life is only beautiful if it is hard. Things won't be good, nice, awesome, worthy, meaning, successful if we never meet failure or obstacles in our life!
"If people do not believe that mathematics is simple, it is only because they do not realize how complicated life is." ~John Louis von Neumann
This is truly indeed! If we are taking mathematics hard with a negative mind set, we will stuck in the sorrowful-mathematics-valley that you never able to climb up!
So, when you feel yourselves having a hard time dealing with maths work, here is another nice quote from my Advanced Functions lecturer,
"This is life!" ~ Ms. Joanne Ho
From my own interpretation, life is only beautiful if it is hard. Things won't be good, nice, awesome, worthy, meaning, successful if we never meet failure or obstacles in our life!
Some useful videos about INVERSE-ing the Exponential Function!
This guy is showing both exponential functions y= bx and x = by that i mentioned is the 5.1 post. starting from 10th minute, he starts to teach the inverse of exponential function.
This young lady focuses on inverse of exponential function. She finishes teaching to transform exponential function into its inverse by 1:47 in the video and continues with inverse function which involve in Logarithm. Ig you find yourselves confused, just watch until 1:47 minute.
I hope these 2 videos help you from the exponential inverse MONSTER! haha! Good night! zzzz....
Source: AlRichards314 and Rip85hotmail, Youtube.
Thursday, 3 November 2011
6.1 The Exponential Function and Its Inverse
The general form of exponential function is y = bx
There are 2 forms if exponential function. First, y = bx where b>0, b≠1
For example, the graph below:
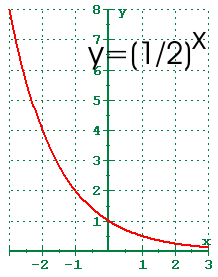
The second form of exponential function is y = bx where b>0
For example, the graph below:
&x=0003)
KEY FEATURES
Domain : {x ∈ R}
Range: {y = R, y>0}
y-intercept of 1
horizontal asymptote at y= 0
In conclusion, KEY FEATURES of exponential function are
- it has a repeating pattern of inite differences
- in the interval of b>1, the rate of change is increasing proportional to the function
- whereas, in the interval of 0<b<1, the rate of change is decreasing proportional to the function.
Now you know all the key features of exponential function. Here we move on to the inverse of exponential function!
The inverse function of y = bx x = by

There are 2 forms if exponential function. First, y = bx where b>0, b≠1
For example, the graph below:
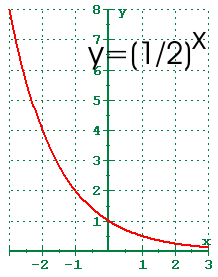
The second form of exponential function is y = bx where b>0
For example, the graph below:
KEY FEATURES
Domain : {x ∈ R}
Range: {y = R, y>0}
y-intercept of 1
horizontal asymptote at y= 0
In conclusion, KEY FEATURES of exponential function are
- it has a repeating pattern of inite differences
- in the interval of b>1, the rate of change is increasing proportional to the function
- whereas, in the interval of 0<b<1, the rate of change is decreasing proportional to the function.
Now you know all the key features of exponential function. Here we move on to the inverse of exponential function!
The inverse function of y = bx x = by

If you observe it, you actually can find that inverse exponential is reflected at the line y = x.
Please take notes that it's KEY FEATURES are different from exponential function.
Domain: { x ∈ R, x > 0 }
Range: {y ∈ R}
Please take notes that it's KEY FEATURES are different from exponential function.
Domain: { x ∈ R, x > 0 }
Range: {y ∈ R}
Vertical Asymptote at x = 0
For more information about logarithm and it's inverse, go to
this link, hope it helps!
For more information about logarithm and it's inverse, go to
this link, hope it helps!
Tuesday, 1 November 2011
It's back and for better!
Hey, hey, hey~ Yu Hang's back for Advanced Function's blog!
You know what, I don't really like Logarithm... I used to have fear with it. When i was form 4 and form 5 i had a great trauma with it. I used to have a mindset that it's real tough and i just don't happen to understand what LOGARITHM means to me.
Even when we started Chapter 6. I had a bit of nervous~ But, things don't really go too scary, creepy, haunting.... as i think! haha! I guess, my mind GREW! yeah!! maybe... Ms. Joanne's methodology works on me! anyway, I'm happy.
Logarithm? no wooooories~ come and fight! ACHA! HIYAK!

This is what I feel now. I failed quite some times last time when I was doing my Logarithm chapter in high school. But, now, I believed that I know it better!
Come on, let's go through the chapter 6 - Exponential and Logarithmic Function together! I hope I can give you some helpful information! Have a great day~
You know what, I don't really like Logarithm... I used to have fear with it. When i was form 4 and form 5 i had a great trauma with it. I used to have a mindset that it's real tough and i just don't happen to understand what LOGARITHM means to me.
Even when we started Chapter 6. I had a bit of nervous~ But, things don't really go too scary, creepy, haunting.... as i think! haha! I guess, my mind GREW! yeah!! maybe... Ms. Joanne's methodology works on me! anyway, I'm happy.
Logarithm? no wooooories~ come and fight! ACHA! HIYAK!

This is what I feel now. I failed quite some times last time when I was doing my Logarithm chapter in high school. But, now, I believed that I know it better!
Come on, let's go through the chapter 6 - Exponential and Logarithmic Function together! I hope I can give you some helpful information! Have a great day~
Subscribe to:
Comments (Atom)


